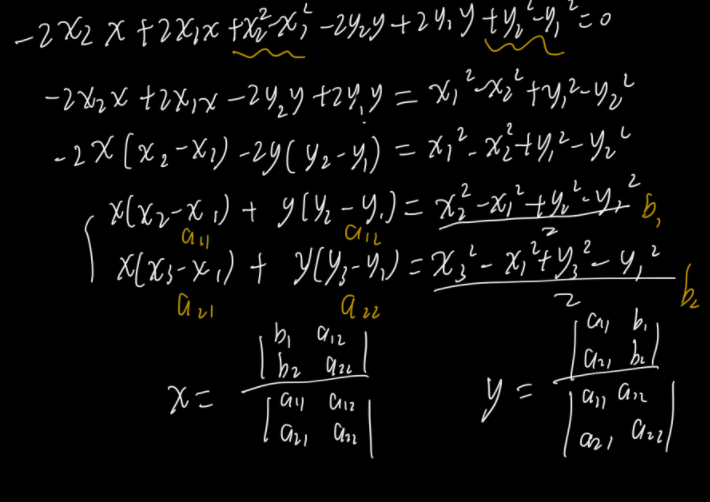此部分由我前 队友完成。浏览体验可能会有所不同因为水平比我强
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #define Vector Point #define PI acos(-1) int sgn (double x) if (fabs (x) < ZERO) return 0 ; else if (x > 0 ) return 1 ; else return -1 ; } struct Point { double x, y; Point (double x = 0 , double y = 0 ) : x (x), y (y) { } Point operator + (Point & b) { return Point (x + b.x, y + b.y); } Point operator - (Point & b) { return Point (x - b.x, y - b.y); } Point operator * (double k) { return Point (x * k, y * k); } Point operator / (double k) {return Point (x / k, y / k); } bool operator < (Point b) { return equals (x, b.x) ? y < b.y : x < b.x; } bool operator == (Point b) { return equals (x, b.x) && equals (y, b.y); } }; double dot (Vector A, Vector B) return A.x * B.x + A.y * B.y; } double Cross (Vector A, Vector B) return A.x * B.y - A.y * B.x; } double get_length (Point A) return sqrt (dot (A, A)); } double get_angle (Point A, Point B) return acos (dot (A, B) / get_length (A) / get_length (B)); } Point rotate (Point A, double theta) { return Point (A.x * cos (theta) + A.y * sin (theta), -A.x * sin (theta) + A.y * cos (theta)); } int relation (Point A, Point B, Point C) ll c = Cross (C - A, B - A); return sgn (c); } bool onSegment (Point A, Point B, Point C) return relation (A, B, C) == 0 && sgn (dot (C - A, C - B)) <= 0 ; } double dis2Line (Point A, Point B, Point C) Vector v1 = B - A, v2 = C - A; return fabs (Cross (v1, v2) / get_length (v1)); } double dis2Segment (Point A, Point B, Point C) if (A == B) return get_length (C - A); Vector v1 = B - A, v2 = C - A, v3 = C - B; if (sgn (dot (v1, v2)) < 0 ) return get_length (v2); if (sgn (dot (v1, v3)) < 0 ) return get_length (v3); return dis2Line (A, B, C); }
c 2 = a 2 + b 2 − 2 × a × b × cos ( C ) c^2=a^2+b^2-2\times a \times b\times \cos (C) c 2 = a 2 + b 2 − 2 × a × b × cos ( C )
p = ( a + b + c ) 2 p=\frac{(a+b+c)}2 p = 2 ( a + b + c )
S △ A B C = p ( p − a ) × ( p − b ) × ( p − c ) S_{\triangle ABC}=\sqrt{p(p-a)\times (p-b)\times (p-c)} S △ A B C = p ( p − a ) × ( p − b ) × ( p − c )
A → ⋅ B → = ∣ A → ∣ ∣ B → ∣ cos ( θ ) \overrightarrow A·\overrightarrow B = |\overrightarrow A||\overrightarrow B|\cos(\theta) A ⋅ B = ∣ A ∣ ∣ B ∣ cos ( θ )
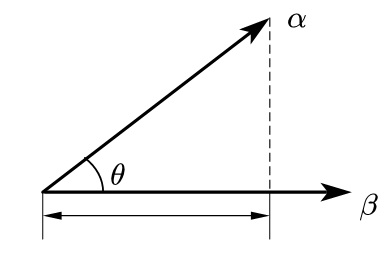
(1) 几何意义 :向量A → \overrightarrow A A B → \overrightarrow B B B → \overrightarrow B B
(2) 公式推导
定义向量c → = a → − b → \overrightarrow c=\overrightarrow a-\overrightarrow b c = a − b
c 2 = a 2 + b 2 − 2 × ∣ a → ∣ ∣ b → ∣ cos θ c^2=a^2+b^2-2\times |\overrightarrow a||\overrightarrow b|\cos \theta c 2 = a 2 + b 2 − 2 × ∣ a ∣ ∣ b ∣ cos θ
即( a → − b → ) ⋅ ( a → − b → ) = a 2 + b 2 − 2 a → ⋅ b → = a 2 + b 2 − 2 × ∣ a → ∣ ∣ b → ∣ cos θ (\overrightarrow a -\overrightarrow b)·(\overrightarrow a - \overrightarrow b)=a^2+b^2-2\overrightarrow a·\overrightarrow b=a^2+b^2-2\times |\overrightarrow a||\overrightarrow b|\cos \theta ( a − b ) ⋅ ( a − b ) = a 2 + b 2 − 2 a ⋅ b = a 2 + b 2 − 2 × ∣ a ∣ ∣ b ∣ cos θ
则a → ⋅ b → = ∣ a → ∣ ∣ b → ∣ cos θ \overrightarrow a ·\overrightarrow b=|\overrightarrow a||\overrightarrow b|\cos \theta a ⋅ b = ∣ a ∣ ∣ b ∣ cos θ
(3) 代码实现
1 2 3 4 double dot (Point A, Point B) return A.x * B.x + A.y * B.y; }
A → × B → = ∣ A → ∣ ∣ B → ∣ sin ( θ ) \overrightarrow A\times \overrightarrow B = |\overrightarrow A||\overrightarrow B|\sin(\theta) A × B = ∣ A ∣ ∣ B ∣ sin ( θ )
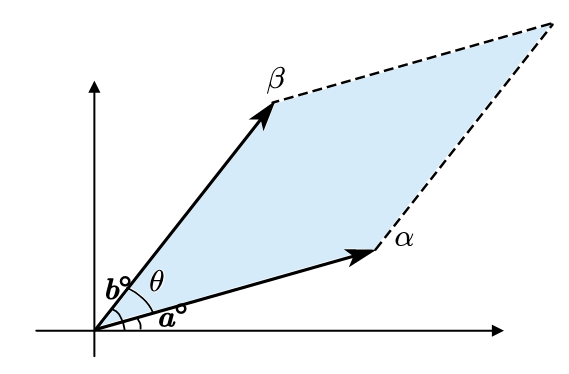
(1) 几何意义 :向量A → \overrightarrow A A B → \overrightarrow B B B → \overrightarrow B B A → \overrightarrow A A
(2) 公式推导 $S=|\alpha|\times|\beta|\times \sin(b-a)= |\alpha|\times |\beta|\times (\sin b\times \cos a-\cos b \times \sin a)\=(|\alpha|\cos a)(|\beta|\sin b)-(|\alpha|\sin a)(|\beta| \cos b)=A.x\times B.y - A.y\times B.x $
(3) 代码实现 1 2 3 4 double Cross (Vector A, Vector B) return A.x * B.y - A.y * B.x; }
1 2 3 4 double get_length (Point A) return sqrt (dot (A, A)); }
θ = arccos ( a → ⋅ b → ∣ a → ∣ ∣ b → ∣ ) \theta=\arccos(\frac{\overrightarrow a·\overrightarrow b}{|\overrightarrow a||\overrightarrow b|}) θ = arccos ( ∣ a ∣ ∣ b ∣ a ⋅ b )
余弦公式没啥好说的0.0
1 2 3 4 double get_angle (Point A, Point B) return acos (dot (A, B) / get_length (A) / get_length (B)); }
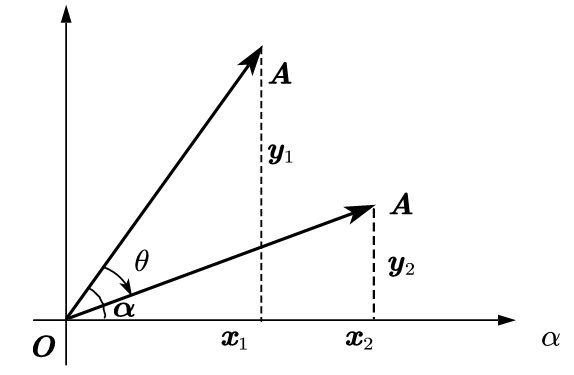
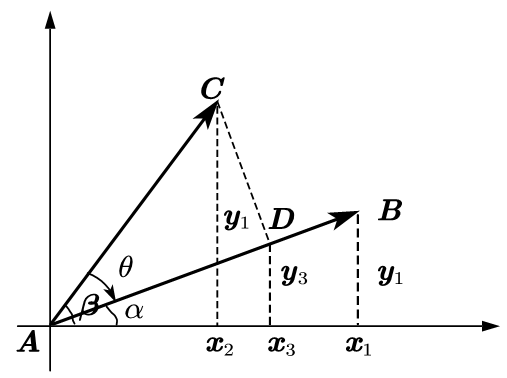
A → \overrightarrow A A θ \theta θ
x 2 = O A × cos ( α − θ ) = O A × ( cos α cos θ + sin α sin θ ) = x 1 × cos θ + y 1 × sin θ x_2=OA\times \cos(\alpha -\theta)=OA\times(\cos \alpha \cos \theta+\sin\alpha \sin \theta)=x_1\times \cos \theta+y_1\times \sin \theta x 2 = O A × cos ( α − θ ) = O A × ( cos α cos θ + sin α sin θ ) = x 1 × cos θ + y 1 × sin θ
y 2 = O A × sin ( α − θ ) = O A × ( sin α cos θ − cos α sin θ ) = − x 1 × sin θ + y 1 × cos θ y_2=OA\times \sin(\alpha -\theta)=OA\times(\sin \alpha \cos \theta-\cos\alpha \sin \theta)=-x_1\times \sin \theta+y_1\times \cos \theta y 2 = O A × sin ( α − θ ) = O A × ( sin α cos θ − cos α sin θ ) = − x 1 × sin θ + y 1 × cos θ
1 2 3 4 Point rotate (Point A, double theta) { return Point (A.x * cos (theta) + A.y * sin (theta), -A.x * sin (theta) + A.y * cos (theta)); }
a x + b y + c = 0 ax+by+c=0 a x + b y + c = 0
{ x = x 0 + m t y = y 0 + n t \begin{cases} x=x_0+mt \\ y=y_0+nt \end{cases} { x = x 0 + m t y = y 0 + n t
设直线L L L M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M 0 ( x 0 , y 0 ) s → = { m , n } \overrightarrow s=\{m,n\} s = { m , n } L L L M M M L L L M 0 M → = { x − x 0 , y − y 0 } \overrightarrow {M_0M}=\{x-x_0,y-y_0\} M 0 M = { x − x 0 , y − y 0 } M 0 M → / / s → \overrightarrow {M_0M} ~//~~ \overrightarrow s M 0 M / / s
t = x − x 0 m = y − y 0 n t=\frac{x-x_0}m =\frac{y-y_0}n t = m x − x 0 = n y − y 0 点向式方程 为:
x − x 0 m = y − y 0 n \frac{x-x_0}m =\frac{y-y_0}n m x − x 0 = n y − y 0 m , n m,n m , n
则方程组{ x = x 0 + m t y = y 0 + n t , t ∈ R \begin{cases} x=x_0+mt \\ y=y_0+nt \end{cases},t\in\R { x = x 0 + m t y = y 0 + n t , t ∈ R
称为直线的参数方程
y = k x + b y=kx+b y = k x + b
x − x 1 x 2 − x 1 = y − y 1 y 2 − y 1 \frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} x 2 − x 1 x − x 1 = y 2 − y 1 y − y 1
1 2 3 int getPoint (Point A) return abs (gcd (A.x, A.y)) + 1 ; }
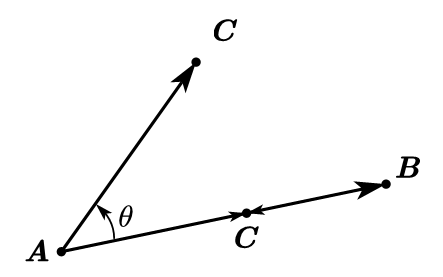
判断点C C C A B AB A B x = A C → × A B → x=\overrightarrow {AC}\times \overrightarrow {AB} x = A C × A B
1 2 3 4 5 6 int relation (Point A, Point B, Point C) ll c = Cross (C - A, B - A); return sgn (c); }
首先应满足点C C C A B AB A B C C C A B AB A B
即:A C → × A B → = 0 , A C → ⋅ B C → ≤ 0 \overrightarrow {AC}\times \overrightarrow {AB}=0,\overrightarrow{AC}·\overrightarrow {BC}\leq 0 A C × A B = 0 , A C ⋅ B C ≤ 0
1 2 3 4 5 bool onSegment (Point A, Point B, Point C) return relation (A, B, C) == 0 && sgn (dot (C - A, C - B)) <= 0 ; }
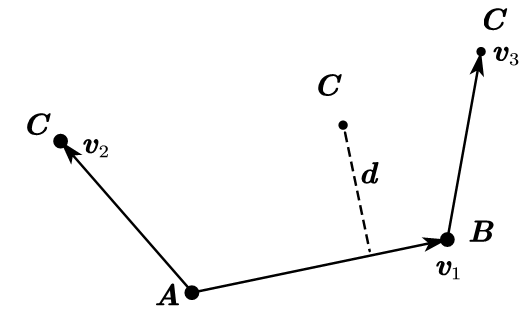
S A B C D = v 1 → × v 2 → = d × ∣ v 2 → ∣ S_{ABCD}=\overrightarrow {v_1}\times \overrightarrow {v_2}=d\times |\overrightarrow {v_2}| S A B C D = v 1 × v 2 = d × ∣ v 2 ∣ ∴ d = v 1 → × v 2 → ∣ v 1 → ∣ \therefore d=\frac{\overrightarrow {v_1}\times \overrightarrow {v_2}}{|\overrightarrow {v_1}|} ∴ d = ∣ v 1 ∣ v 1 × v 2
1 2 3 4 5 double dis2Line (Point A, Point B, Point C) Vector v1 = B - A, v2 = C - A; return fabs (Cross (v1, v2) / get_length (v1)); }
C C C A B AB A B
注意:A点必须在B点的左边,否则会计算错误
当A B AB A B g e t _ d i s ( A , C ) get\_dis(A,C) g e t _ d i s ( A , C ) C C C A B AB A B d i s 2 L i n e ( C , A , B ) dis2Line(C,A,B) d i s 2 L i n e ( C , A , B )
当C C C ∣ v → 2 ∣ |\overrightarrow v_2| ∣ v 2 ∣ C C C ∣ v → 1 ∣ |\overrightarrow v_1| ∣ v 1 ∣
1 2 3 4 5 6 7 8 double dis2Segment (Point A, Point B, Point C) if (A == B) return get_length (C - A); Vector v1 = B - A, v2 = C - A, v3 = C - B; if (sgn (dot (v1, v2)) < 0 ) return get_length (v2); if (sgn (dot (v1, v3)) < 0 ) return get_length (v3); return dis2Line (A, B, C); }
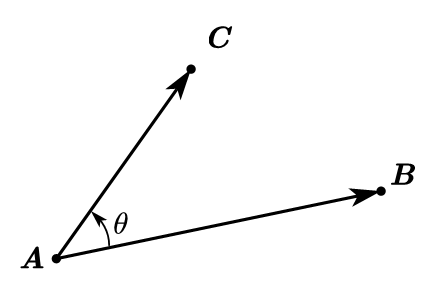
如图点D D D O A → + A D → \overrightarrow {OA} +\overrightarrow {AD} O A + A D A D → \overrightarrow {AD} A D
∣ A D → ∣ = ∣ A C → ∣ × cos θ |\overrightarrow {AD}|=|\overrightarrow {AC}|\times \cos \theta ∣ A D ∣ = ∣ A C ∣ × cos θ
∴ t = ∣ A D → ∣ ∣ A B → ∣ = A B → ⋅ A C → ∣ A B → ∣ 2 = A B → ⋅ A C → A B → ⋅ A B → \therefore t=\frac{|\overrightarrow {AD}|}{|\overrightarrow {AB}|}=\frac{\overrightarrow {AB}·\overrightarrow {AC}}{|\overrightarrow {AB}|^2}=\frac{\overrightarrow {AB}·\overrightarrow {AC}}{\overrightarrow {AB}·\overrightarrow {AB}} ∴ t = ∣ A B ∣ ∣ A D ∣ = ∣ A B ∣ 2 A B ⋅ A C = A B ⋅ A B A B ⋅ A C
A D → = O A → + A B → × t \overrightarrow {AD}=\overrightarrow {OA}+\overrightarrow {AB}\times t A D = O A + A B × t
1 2 3 4 5 6 Point projection2Line (Point A, Point B, Point C) { Point v = B - A; v = v * (dot (v, C - A) / dot (v, v)); return A + v; }
两直线之间的关系: 用来判断两个线段之间的关系。
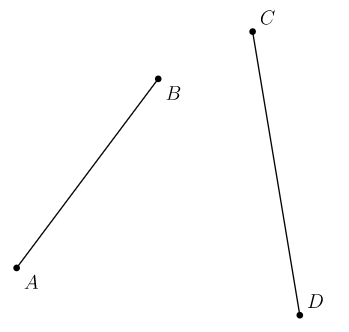
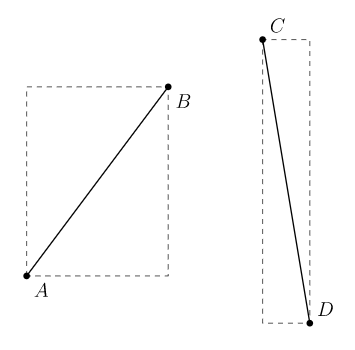
规定「一条线段的区域」为以这条线段为对角线的,各边均与某一坐标轴平行的矩形所占的区域,那么可以发现,如果两条线段没有公共区域,则这两条线段一定不相交。比如有以下两条线段,它们占用的区域是这样的:
于是可以快速地判断出来这两条线段不相交。
这就是 快速排斥实验 。上述情况称作 未通过快速排斥实验 。
未通过快速排斥实验是两线段无交点的 充分不必要条件 ,我们还需要进一步判断。
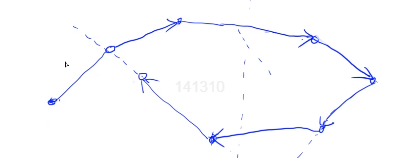
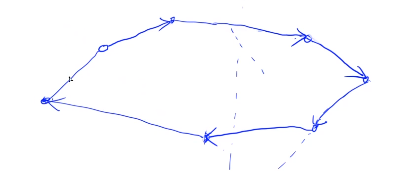
因为两线段 相交, 线段的两个端点一定分布在 线段所在直线两端;同理, 线段的两个端点一定分布在 线段所在直线两端。我们可以直接判断一条线段的两个端点相对于另一线段所在直线的位置关系,如果不同,则两线段相交,反之则不相交。我们可以利用 3.1 中的知识帮助我们判断直线与点的位置关系。
这就是 跨立实验 ,如果对于两线段 , 线段的两个端点分布在 线段所在直线的两侧,且 线段的两个端点分布在 线段所在直线的两侧,我们就说 两线段 通过了跨立实验 ,即两线段相交。
注意到当两条线段共线但不相交时也可以通过跨立实验,因此想要准确判断还需要与快速排斥实验结合。 (y总你的模板又错辣,自己又重写的应该是对的)
1 2 3 4 5 6 7 bool segmentIntersection (Point a1, Point a2, Point b1, Point b2) int c1 = relation (b1, b2, a1), c2 = relation (b1, b2, a2); int c3 = relation (a1, a2, b1), c4 = relation (a1, a2, b2); if (c1 * c2 < 0 && c3 * c4 < 0 ) return true ; return onSegment (b1, b2, a1) || onSegment (b1, b2, a2); }
1 2 3 4 5 6 7 8 9 10 Point getCrossPoint_Line (Line s1, Line s2) { Vector v1, v2; v1 = s1.p2 - s1.p1, v2 = s2.p2 - s2.p1; Vector u = s1.p1 - s2.p1; double t = Cross (v2, u) / Cross (v1, v2); Point x = v1 * t; return s1.p1 + x; }
直接看全家桶。
叉积,放在多边形公式里一起写
海伦公式求面积
p = ( a + b + c ) 2 p=\frac{(a+b+c)}2 p = 2 ( a + b + c )
S △ A B C = p ( p − a ) × ( p − b ) × ( p − c ) S_{\triangle ABC}=\sqrt{p(p-a)\times (p-b)\times (p-c)} S △ A B C = p ( p − a ) × ( p − b ) × ( p − c )
(1) 外心,外接圆圆心 (2) 内心,内切圆圆心 (3) 垂心 (4) 重心
通常按逆时针 存储所有点
(1) 多边形 :由在同一平面且不再同一直线上的多条线段首尾顺次连接且不相交所组成的图形叫多边形
(2) 简单多边形 :简单多边形是除相邻边外其它边不相交的多边形
(3) 凸多边形 :过多边形的任意一边做一条直线,如果其他各个顶点都在这条直线的同侧,则把这个多边形叫做凸多边形。任意凸多边形外角和均为360 ° 360° 3 6 0 ° 任意凸多边形内角和为( n − 2 ) × 180 ° (n−2)\times 180° ( n − 2 ) × 1 8 0 °
求多边形面积(不一定是凸多边形,凹多边形也可以)
1 2 3 4 5 6 7 8 9 10 typedef vector<Point> Polygon;double get_area (Polygon s) int n = s.size (); double res = 0 ; for (int i=0 ;i<n;++i){ res += fabs (Cross (s[i], s[(i + 1 ) % n]) / 2 ); } return res; }
判断点与多边形(不一定是凸多边形)的关系
射线法 :从该点任意做一条和所有边都不平行的射线。交点个数为偶数,则在多边形外,为奇数,则在多边形内。
转角法
判断点在凸多边形内 :只需判断点是否在所有边的左边(逆时针存储多边形)
皮克定理指的是一个计算点阵中顶点在格点上的多边形面积公式。该公式可表示为S = a + b 2 − 1 S=a+\frac b 2-1 S = a + 2 b − 1 a a a b b b S S S
证明:不会证明,略。
例题hdu1706
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #define ll long long int a1, b1, a2, b2, a3, b3;struct Point { int x, y; Point (int x = 0 , int y = 0 ) : x (x), y (y) { } Point operator + (Point & b) { return Point (x + b.x, y + b.y); } Point operator - (Point & b) { return Point (x - b.x, y - b.y); } Point operator * (int k) { return Point (x * k, y * k); } Point operator / (int k) {return Point (x / k, y / k); } bool operator < (Point b) { return x == b.x ? y < b.y : x < b.x; } }; int gcd (int a, int b) return b ? gcd (b, a % b) : a; } int Cross (Point A, Point B) return abs (A.x * B.y - A.y * B.x); } int getPoint (Point A) return abs (gcd (A.x, A.y)) + 1 ; } void solve () Point A = Point (a1, b1), B = Point (a2, b2), C = Point (a3, b3); int area = Cross (B - A, C - A); int ab = getPoint (B - A), bc = getPoint (B - C), ac = getPoint (C - A); int b = ab + bc + ac - 3 ; int res = (area + 2 - b) / 2 ; printf ("%d\n" , res); } int main (void ) while (~scanf ("%d%d%d%d%d%d" , &a1, &b1, &a2, &b2, &a3, &b3)){ if (a1 == 0 && b1 == 0 && a2 == 0 && b2 == 0 ) return 0 ; solve (); } return 0 ; }
累了,看计算几何全家桶吧orz。
在平面内取一个定点O O O O x Ox O x M M M ρ ρ ρ O M OM O M r r r θ θ θ O x Ox O x O M OM O M ρ ρ ρ M M M θ θ θ M M M ( ρ , θ ) (ρ,θ) ( ρ , θ ) M M M
那么给定平面上的一些点,把它们按照一个选定的中心点排成顺(逆)时针。
1 2 3 4 5 6 7 8 using Points = vector<Point>;double theta (auto p) return atan2 (p.y, p.x); } void psort (Points &ps, Point c = O) sort (ps.begin (), ps.end (), [&](auto p1, auto p2) { return lt (theta (p1 - c), theta (p2 - c)); }); }
1 2 3 4 5 6 7 int qua (auto p) return lt (p.y, 0 ) << 1 | lt (p.x, 0 ) ^ lt (p.y, 0 ); } void psort (Points &ps, Point c = O) sort (ps.begin (), ps.end (), [&](auto v1, auto v2) { return qua (v1 - c) < qua (v2 - c) || qua (v1 - c) == qua (v2 - c) && lt (cross (v1 - c, v2 - c), 0 ); }); }
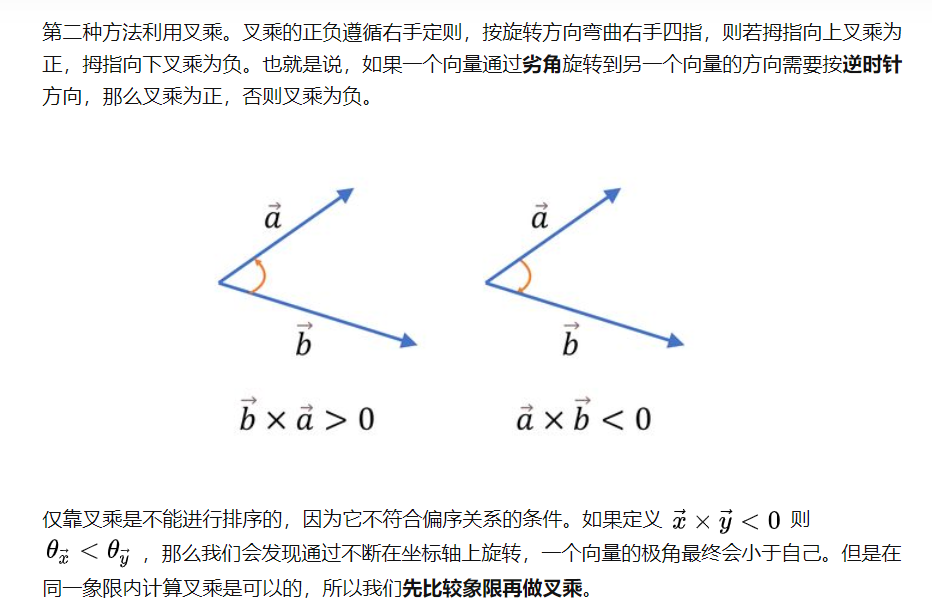
我们用0、1、2、3来表示第一、二、三、四象限。这种方法常数可能稍微大一点,但是精度比较好,如果坐标都是整数的话是完全没有精度损失的。另外一定要注意,在角度可能很小时,不要用比较余弦的方法比较角度,那样精度会有严重问题。
这篇博客已经介绍的非常详细了,但是太太太长了,放链接
https://www.luogu.com.cn/blog/ShineEternal/convex-hull
凸包是围住所有点的面积最小,周长也最小的凸多边形。
用一个单调栈来维护凸包形状。
将点排序,x为第一关键字,y为第二关键字。
分两步,从左至右维护上半部分(上链);从右至左维护下半部分(下链)。
维护上链时,首先加入前两个点;维护下链时,首先加入最后两个点。每次看新加进来的点C C C A B → \overrightarrow{AB} A B B C BC B C B B B A C → \overrightarrow {AC} A C 如果C在A B → \overrightarrow{AB} A B C C C 。
注意,在最后一步一定要再用栈底元素更新一遍,否则无法构成凸包。更新这两个边界点非常重要!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 inline Polygon andrewScan (Polygon p) Polygon u, d; if (p.size () < 3 ) return p; sort (p.begin (), p.end ()); u.pb (p[0 ]); u.pb (p[1 ]); d.pb (p[p.size () - 1 ]); d.pb (p[p.size () - 2 ]); for (int i = 2 ; i < p.size (); i++) { for (int k = u.size (); k >= 2 && ccw (u[k - 2 ], u[k - 1 ], p[i]) != C; k--) u.pop_back (); u.pb (p[i]); } for (int i = p.size () - 3 ; ~i; i--) { for (int k = d.size (); k >= 2 && ccw (d[k - 2 ], d[k - 1 ], p[i]) != C; k--) d.pop_back (); d.pb (p[i]); } reverse (d.begin (), d.end ()); for (int i = u.size () - 2 ; i; i--) d.pb (u[i]); return d; } int main (void ) scanf ("%d" , &n); Polygon q (n) ; for (int i = 0 ; i < n; i ++ ) scanf ("%lf%lf" , &q[i].x, &q[i].y); Polygon d = andrewScan (q); double res = get_dis (d[0 ], d.back ()); for (int i=1 ;i<d.size ();++i){ res += get_dis (d[i], d[i - 1 ]); } printf ("%.2f\n" , res); return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 #include <iostream> #include <cstdio> #include <algorithm> #include <cstring> #include <cmath> #define pf(x) (x) * (x) #define eps 1e-12 using namespace std;int n;struct point { double x; double y; }o, a[100000 + 10 ]; double r;double dis (point a, point b) return sqrt (pf (a.x - b.x) + pf (a.y - b.y)); } void get (point a, point b, point c) double a11 = b.x - a.x; double a12 = b.y - a.y; double b1 = (pf (b.x) - pf (a.x) + pf (b.y) - pf (a.y)) * 0.5 ; double a21 = c.x - a.x; double a22 = c.y - a.y; double b2 = (pf (c.x) - pf (a.x) + pf (c.y) - pf (a.y)) * 0.5 ; o.x = (b1 * a22 - a12 * b2) / (a11 * a22 - a12 * a21); o.y = (a11 * b2 - b1 * a21) / (a11 * a22 - a12 * a21); r = dis (o, a); } int main () cin >> n; for (int i = 1 ; i <= n; i++){ cin >> a[i].x >> a[i].y; } random_shuffle (a + 1 , a + 1 + n); o = a[1 ]; r = 0 ; for (int i = 2 ; i <= n; i++){ if (dis (a[i], o) > r + eps){ o = a[i]; r = 0 ; for (int j = 1 ; j <= i - 1 ; j++){ if (dis (a[j], o) > r + eps){ o.x = (a[i].x + a[j].x) / 2 ; o.y = (a[i].y + a[j].y) / 2 ; r = dis (o, a[j]); for (int k = 1 ; k <= j - 1 ; k++){ if (dis (a[k], o) > r + eps){ get (a[i], a[j], a[k]); } } } } } } printf ("%.10lf\n%.10lf %.10lf" , r, o.x, o.y); return 0 ; }
增量法构造半平面
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 #include <bits/stdc++.h> using namespace std;const double INF = 1e12 ;const double pi = acos (-1.0 );const double eps = 1e-8 ;int sgn (double x) if (fabs (x) < eps) return 0 ; else return x<0 ?-1 :1 ; } struct Point { double x,y; Point () {} Point (double x,double y):x (x),y (y) {} Point operator + (Point B) { return Point (x+B.x,y+B.y); } Point operator - (Point B) { return Point (x-B.x,y-B.y); } Point operator * (double k) { return Point (x*k,y*k); } }; typedef Point Vector;double Cross (Vector A,Vector B) return A.x*B.y - A.y*B.x; } struct Line { Point p; Vector v; double ang; Line () {}; Line (Point p,Vector v):p (p),v (v) { ang=atan2 (v.y,v.x); } bool operator < (Line &L) { return ang<L.ang; } }; bool OnLeft (Line L,Point p) return sgn (Cross (L.v,p-L.p))>0 ; } Point Cross_point (Line a,Line b) Vector u=a.p-b.p; double t=Cross (b.v,u)/Cross (a.v,b.v); return a.p+a.v*t; } vector<Point> HPI (vector<Line> L) int n=L.size (); sort (L.begin (),L.end ()); int first,last; vector<Point> p (n) ; vector<Line> q (n) ; vector<Point> ans; q[first=last=0 ]=L[0 ]; for (int i=1 ; i<n; i++) { while (first<last && !OnLeft (L[i], p[last-1 ])) last--; while (first<last && !OnLeft (L[i], p[first])) first++; q[++last]=L[i]; if (fabs (Cross (q[last].v,q[last-1 ].v)) < eps) { last--; if (OnLeft (q[last],L[i].p)) q[last]=L[i]; } if (first<last) p[last-1 ]=Cross_point (q[last-1 ],q[last]); } while (first<last && !OnLeft (q[first],p[last-1 ])) last--; if (last-first<=1 ) return ans; p[last]=Cross_point (q[last],q[first]); for (int i=first; i<=last; i++) ans.push_back (p[i]); return ans; } double Polygon_area (vector<Point> p) int n=p.size (); double area = 0 ; for (int i = 0 ; i < n; i++) area += Cross (p[i],p[(i+1 )%n]); return area/2 ; } int main () int n,m; vector<Line> L; cin>>n; while (n--) { cin>>m; vector<Point> tmp; for (int i=0 ;i<m;i++) { double a,b; scanf ("%lf%lf" ,&a,&b); tmp.push_back (Point (a,b)); } for (int i=0 ;i<m;i++) { L.push_back (Line (tmp[i],tmp[(i+1 )%m]-tmp[i])); } } vector<Point> ans=HPI (L); printf ("%.3f" ,Polygon_area (ans)); return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #include <bits/stdc++.h> #define FOR(i,a,b) for(register int i=(a);i<(b);++i) #define ROF(i,a,b) for(register int i=(a);i>=(b);--i) #define pi pair<int,int> #define mk(a,b) make_pair(a,b) #define mygc(c) (c)=getchar() #define mypc(c) putchar(c) #define fi first #define se second using namespace std;typedef long long ll;typedef double db;const int maxn = 10000 ;const int maxm = 100 ;const int inf = 2147483647 ;typedef long long ll;const double eps = 1e-9 ;const long long INF = 9223372036854775807ll ;ll qpow (ll a,ll b,ll c) {ll ans=1 ;while (b){if (b&1 )ans=ans*a%c;a=a*a%c;b>>=1 ;}return ans;}inline void rd (int *x) int k,m=0 ;*x=0 ;for (;;){mygc (k);if (k=='-' ){m=1 ;break ;}if ('0' <=k&&k<='9' ){*x=k-'0' ;break ;}}for (;;){mygc (k);if (k<'0' ||k>'9' )break ;*x=(*x)*10 +k-'0' ;}if (m)(*x)=-(*x);}inline void rd (ll *x) int k,m=0 ;*x=0 ;for (;;){mygc (k);if (k=='-' ){m=1 ;break ;}if ('0' <=k&&k<='9' ){*x=k-'0' ;break ;}}for (;;){mygc (k);if (k<'0' ||k>'9' )break ;*x=(*x)*10 +k-'0' ;}if (m)(*x)=-(*x);}inline void rd (db *x) scanf ("%lf" ,x);}inline int rd (char c[]) int i,s=0 ;for (;;){mygc (i);if (i!=' ' &&i!='\n' &&i!='\r' &&i!='\t' &&i!=EOF) break ;}c[s++]=i;for (;;){mygc (i);if (i==' ' ||i=='\n' ||i=='\r' ||i=='\t' ||i==EOF) break ;c[s++]=i;}c[s]='\0' ;return s;}inline void rd (int a[],int n) FOR (i,0 ,n)rd (&a[i]);}inline void rd (ll a[],int n) FOR (i,0 ,n)rd (&a[i]);}template <class T , class S > inline void rd (T *x, S *y) rd (x);rd (y);}template <class T , class S , class U > inline void rd (T *x, S *y, U *z) rd (x);rd (y);rd (z);}template <class T , class S , class U , class V > inline void rd (T *x, S *y, U *z, V *w) rd (x);rd (y);rd (z);rd (w);}inline void wr (int x) if (x < 10 ) putchar ('0' + x); else wr (x / 10 ), wr (x % 10 );}inline void wr (int x, char c) int s=0 ,m=0 ;char f[10 ];if (x<0 )m=1 ,x=-x;while (x)f[s++]=x%10 ,x/=10 ;if (!s)f[s++]=0 ;if (m)mypc ('-' );while (s--)mypc (f[s]+'0' );mypc (c);}inline void wr (ll x, char c) int s=0 ,m=0 ;char f[20 ];if (x<0 )m=1 ,x=-x;while (x)f[s++]=x%10 ,x/=10 ;if (!s)f[s++]=0 ;if (m)mypc ('-' );while (s--)mypc (f[s]+'0' );mypc (c);}inline void wr (db x, char c) printf ("%.15f" ,x);mypc (c);}inline void wr (const char c[]) int i;for (i=0 ;c[i]!='\0' ;i++)mypc (c[i]);}inline void wr (const char x[], char c) int i;for (i=0 ;x[i]!='\0' ;i++)mypc (x[i]);mypc (c);}template <class T> inline void wrn (T x) wr (x,'\n' );}template <class T, class S> inline void wrn (T x, S y) wr (x,' ' );wr (y,'\n' );}template <class T, class S, class U> inline void wrn (T x, S y, U z) wr (x,' ' );wr (y,' ' );wr (z,'\n' );}template <class T> inline void wra (T x[], int n) int i;if (!n){mypc ('\n' );return ;}FOR (i,0 ,n-1 )wr (x[i],' ' );wr (x[n-1 ],'\n' );}vector<int >f; int sg[maxn],vis[maxn]; void getSG (int n,int maxx) sort (f.begin (),f.end ()); memset (sg,0 ,sizeof (int )*(n+1 )); FOR (i,1 ,n+1 ){ FOR (j,0 ,f.size ()){ if (f[j]>i)break ; vis[sg[i-f[j]]]=1 ; } FOR (j,0 ,maxx+1 )if (!vis[j]){ sg[i]=j; break ; } FOR (j,0 ,f.size ()){ if (f[j]>i)break ; vis[sg[i-f[j]]]=0 ; } } } int main () f.push_back (1 ); f.push_back (5 ); getSG (100 ,50 ); wra (sg,100 ); }